M. Meyer, A. Devesa, S. Hickel, X.Y. Hu, N.A. Adams (2010)
Journal of Computational Physics 229: 6300-6317. doi: 10.1016/j.jcp.2010.04.040
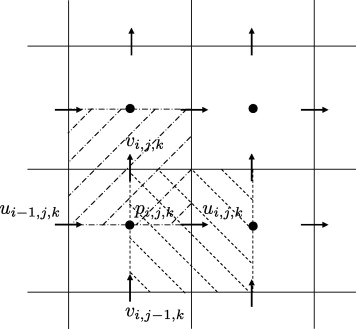
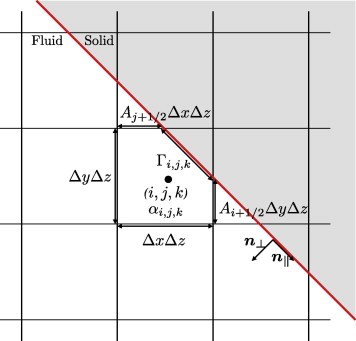
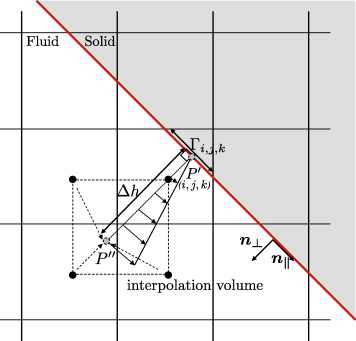
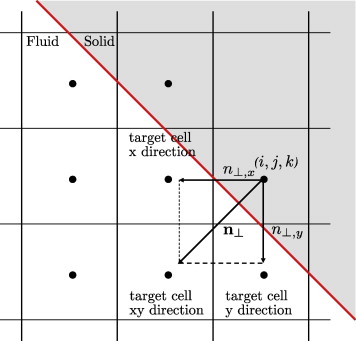
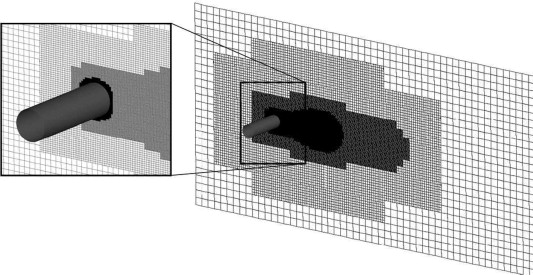
We propose a conservative, second-order accurate immersed interface method for representing incompressible fluid flows over complex three dimensional solid obstacles on a staggered Cartesian grid. The method is based on a finite-volume discretization of the incompressible Navier–Stokes equations which is modified locally in cells that are cut by the interface in such a way that accuracy and conservativity are maintained.
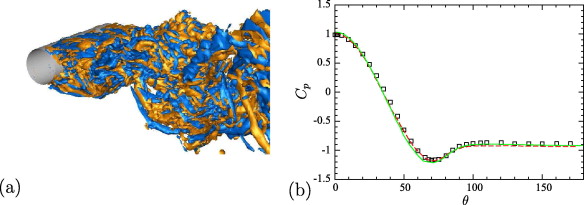
A level-set technique is used for description and tracking of the interface geometry, so that an extension of the method to moving boundaries and flexible walls is straightforward. Numerical stability is ensured for small cells by a conservative mixing procedure. Discrete conservation and sharp representation of the fluid–solid interface render the method particularly suitable for Large-Eddy Simulations of high-Reynolds number flows. Accuracy, second-order grid convergence and robustness of the method is demonstrated for several test cases: inclined channel flow at Re = 20, flow over a square cylinder at Re = 100, flow over a circular cylinder at Re = 40, Re = 100 and Re = 3900, as well as turbulent channel flow with periodic constrictions at Re = 10595.