Y. Zhang, R.P. Dwight, M. Schmelzer, J.F. Gómez, Z.-H. Han, S. Hickel (2021)
Journal of Computational Physics 432: 110153. doi: 10.1016/j.jcp.2021.110153
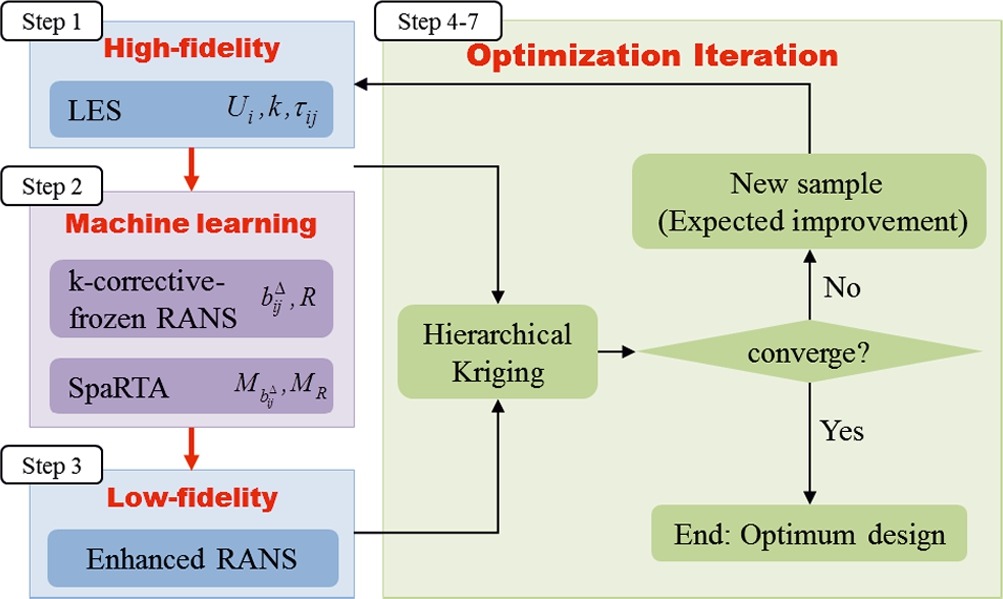
Multi-fidelity optimization methods promise a high-fidelity optimum at a cost only slightly greater than a low-fidelity optimization. This promise is seldom achieved in practice, due to the requirement that low- and high-fidelity models correlate well. In this article, we propose an efficient bi-fidelity shape optimization method for turbulent fluid-flow applications with Large-Eddy Simulation (LES) and Reynolds-averaged Navier-Stokes (RANS) as the high- and low-fidelity models within a hierarchical-Kriging surrogate modelling framework.
Since the LES–RANS correlation is often poor, we use the full LES flow-field at a single point in the design space to derive a custom-tailored RANS closure model that reproduces the LES at that point. This is achieved with machine-learning techniques, specifically sparse regression to obtain high corrections of the turbulence anisotropy tensor and the production of turbulence kinetic energy as functions of the RANS mean-flow. The LES–RANS correlation is dramatically improved throughout the design-space. We demonstrate the effectivity and efficiency of our method in a proof-of-concept shape optimization of the well-known periodic-hill case. Standard RANS models perform poorly in this case, whereas our method converges to the LES-optimum with only two LES samples.