H. Müller, C. Niedermeier, J. Matheis, M. Pfitzner, S. Hickel (2016)
Physics of Fluids 28: 015102. doi: 10.1063/1.4937948
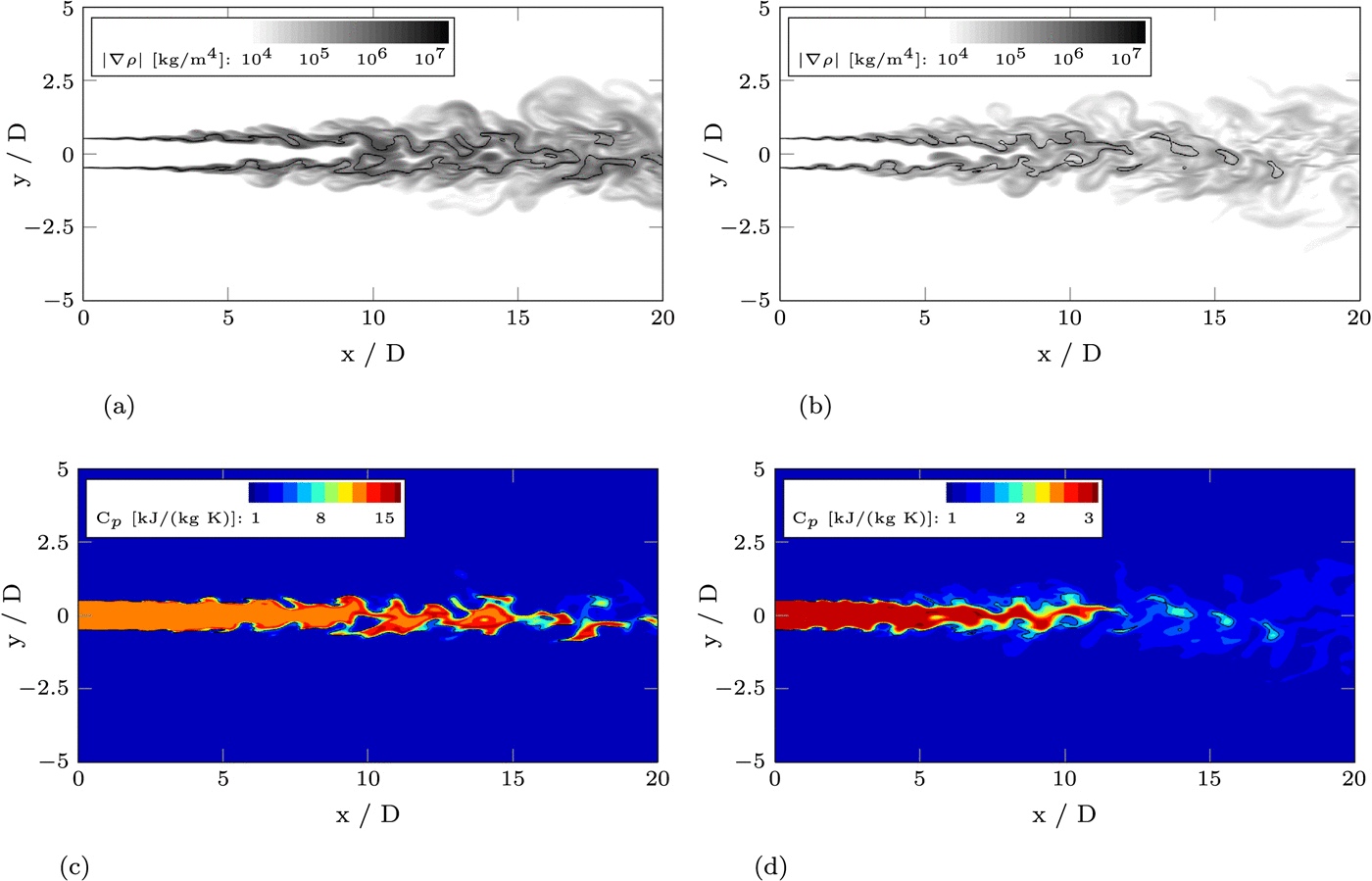
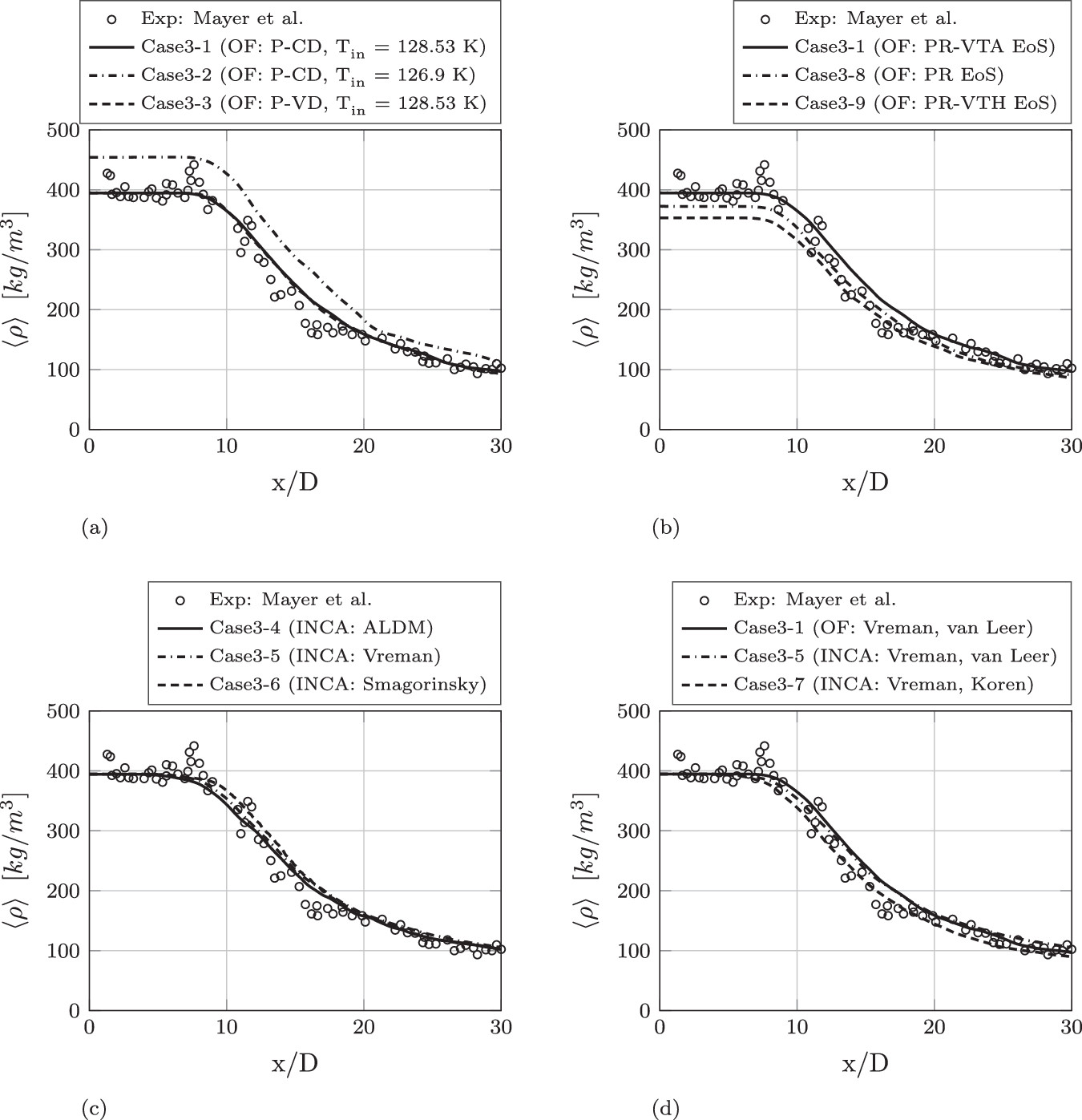
Large-eddy simulations (LES) of cryogenic nitrogen injection into a warm environment at supercritical pressure are performed and real-gas thermodynamics models and subgrid-scale (SGS) turbulence models are evaluated. The comparison of different SGS models — the Smagorinsky model, the Vreman model, and the adaptive local deconvolution method — shows that the representation of turbulence on the resolved scales has a notable effect on the location of jet break-up, whereas the particular modeling of unresolved scales is less important for the overall mean flow field evolution. More important are the models for the fluid’s thermodynamic state.
The injected fluid is either in a supercritical or in a transcritical state and undergoes a pseudo-boiling process during mixing. Such flows typically exhibit strong density gradients that delay the instability growth and can lead to a redistribution of turbulence kinetic energy from the radial to the axial flow direction. We evaluate novel volume-translation methods on the basis of the cubic Peng-Robinson equation of state in the framework of LES. At small extra computational cost, their application considerably improves the simulation results compared to the standard formulation. Furthermore, we found that the choice of inflow temperature is crucial for the reproduction of the experimental results and that heat addition within the injector can affect the mean flow field in comparison to results with an adiabatic injector.