INCA

On the transition between regular and irregular shock patterns of shock-wave/boundary-layer interactions

J. Matheis, S. Hickel (2015)
Journal of Fluid Mechanics 776: 200-234. doi: 10.1017/jfm.2015.319

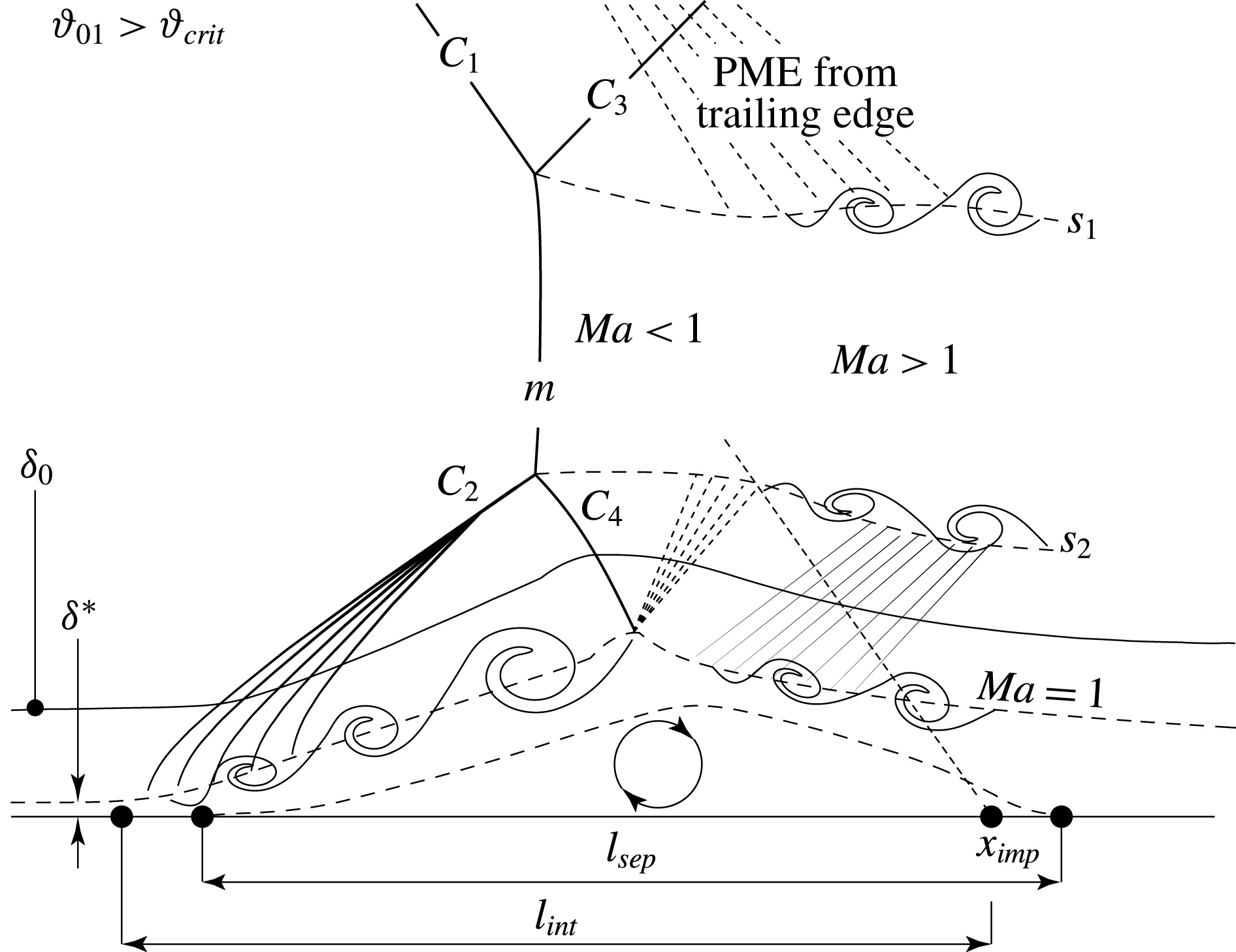
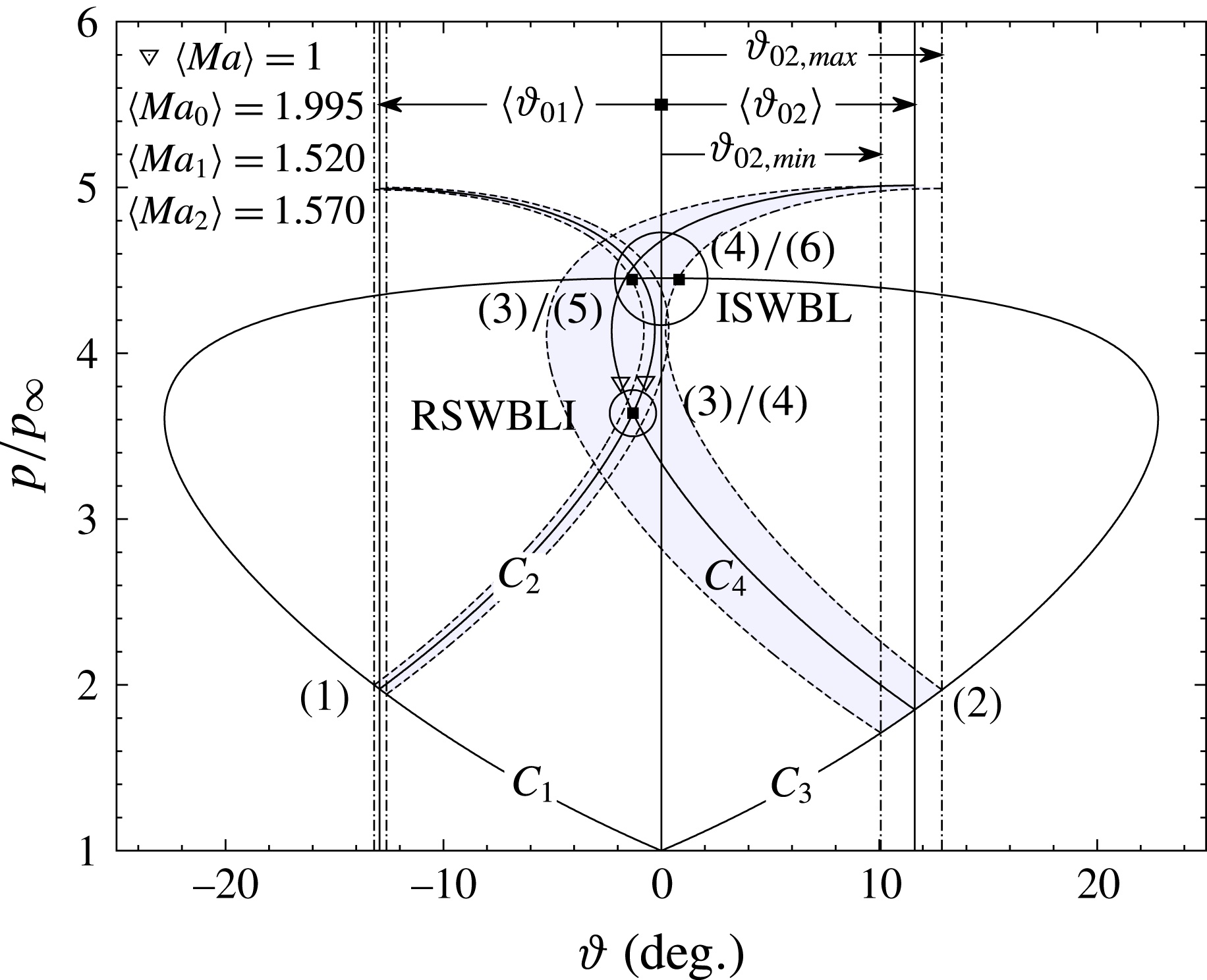
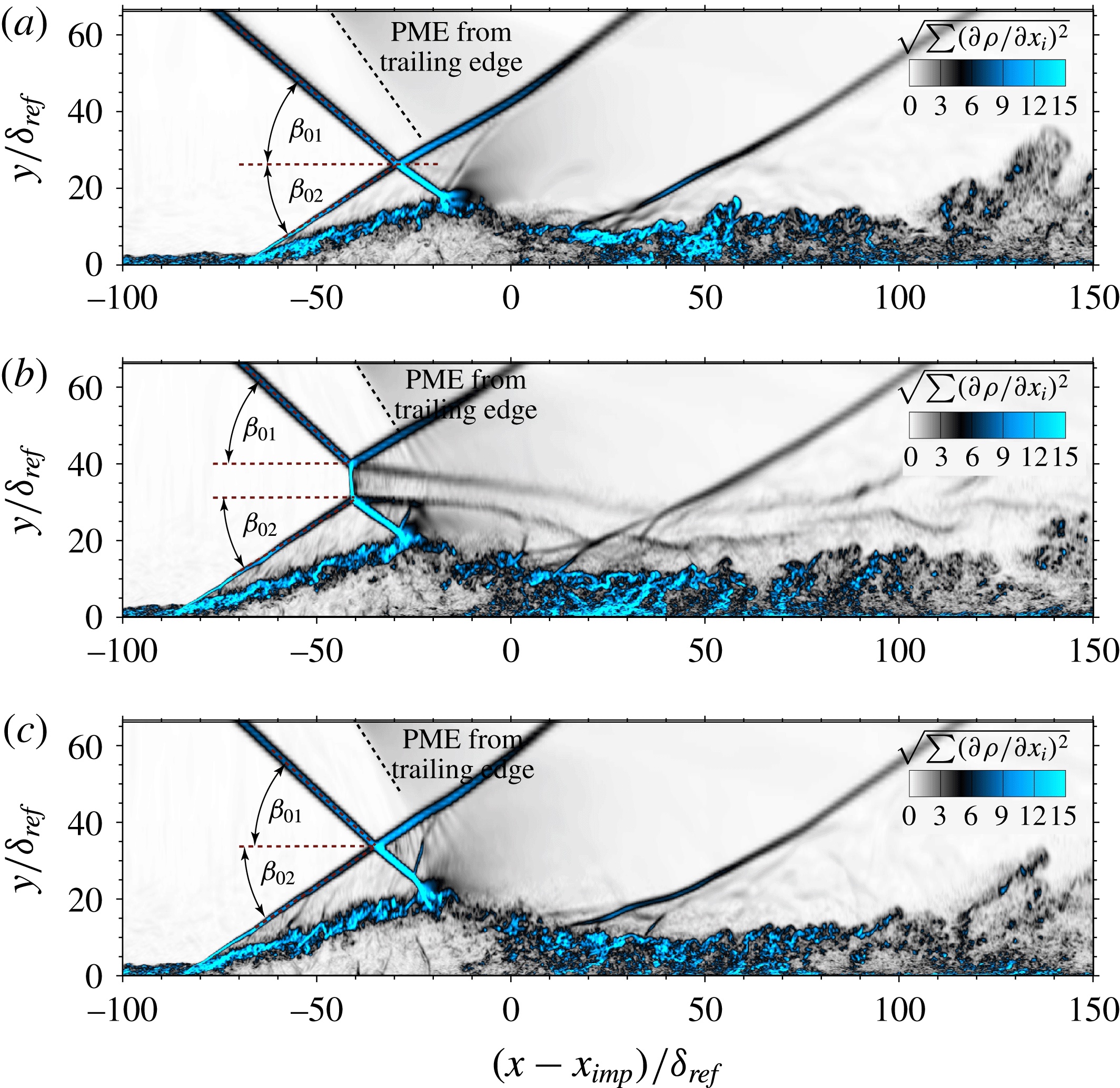
The reflection of strong oblique shock waves at turbulent boundary layers is studied numerically and analytically. A particular emphasis is put on the transition between regular shock-wave/boundary-layer interaction (SWBLI) and Mach reflection (irregular SWBLI). The classical two- and three-shock theory and a generalised form of the free interaction theory are used for the analysis of well-resolved large-eddy simulations (LES) and for the derivation of stability criteria.

We found that at a critical deflection angle across the incident shock wave, the perturbations related to the turbulent boundary layer cause bi-directional transition processes between regular and irregular shock patterns for a free-stream Mach number of Ma = 2 . Computational results show that the mean deflection angle across the separation shock is decoupled from the incident shock wave and can be accurately modelled by the generalised free interaction theory. On the basis of these observations, and the von Neumann and detachment criteria for the asymmetric intersection of shock waves, we derive the critical incident shock deflection angles at which the shock pattern may/must become irregular. Numerical data for a free-stream Mach number of Ma = 3 confirm the existence of the dual-solution domain predicted by theory. 

 

Schematic of an irregular shock-wave / boundary-layer interaction (SWBLI), where a Mach stem forms at the intersection of incident shock and separation shock.  

 

Shock polar representation of unsteady effects on the intersection of incident shock C1 and separation shock C2 for a Ma = 2 case. Numbering of the states according to the schematic above. The solid lines (——) depict the polars in a time-averaged context, while the dashed lines (- - - -) correspond to the observed maximum and minimum deflections across C1 and C2, and enclose the gray shaded region of possible quasi-steady states.

 

Numerical schlieren visualizations of instantaneous interaction at Ma = 3: (a) regular interaction at wedge angle 𝜗01= 22.5° and shock angle β01= 40.5°; (b) irregular interaction at wedge angle 𝜗01= 24.5° and shock angle β01= 42.8°; (c) regular interaction at the same flow conditions with 𝜗01= 24.5° and shock angle β01= 42.8°. The separation shock angles are (a) β02= 32.5°, (b) β02= 31.7°, (c) β02= 34.3°.

Publications