INCA - Rossby-number effects on columnar eddy formation and the energy dissipation law in homogeneous rotating turbulence

T. Pestana, S. Hickel (2020)
Journal of Fluid Mechanics 885: A7. doi: 10.1017/jfm.2019.976

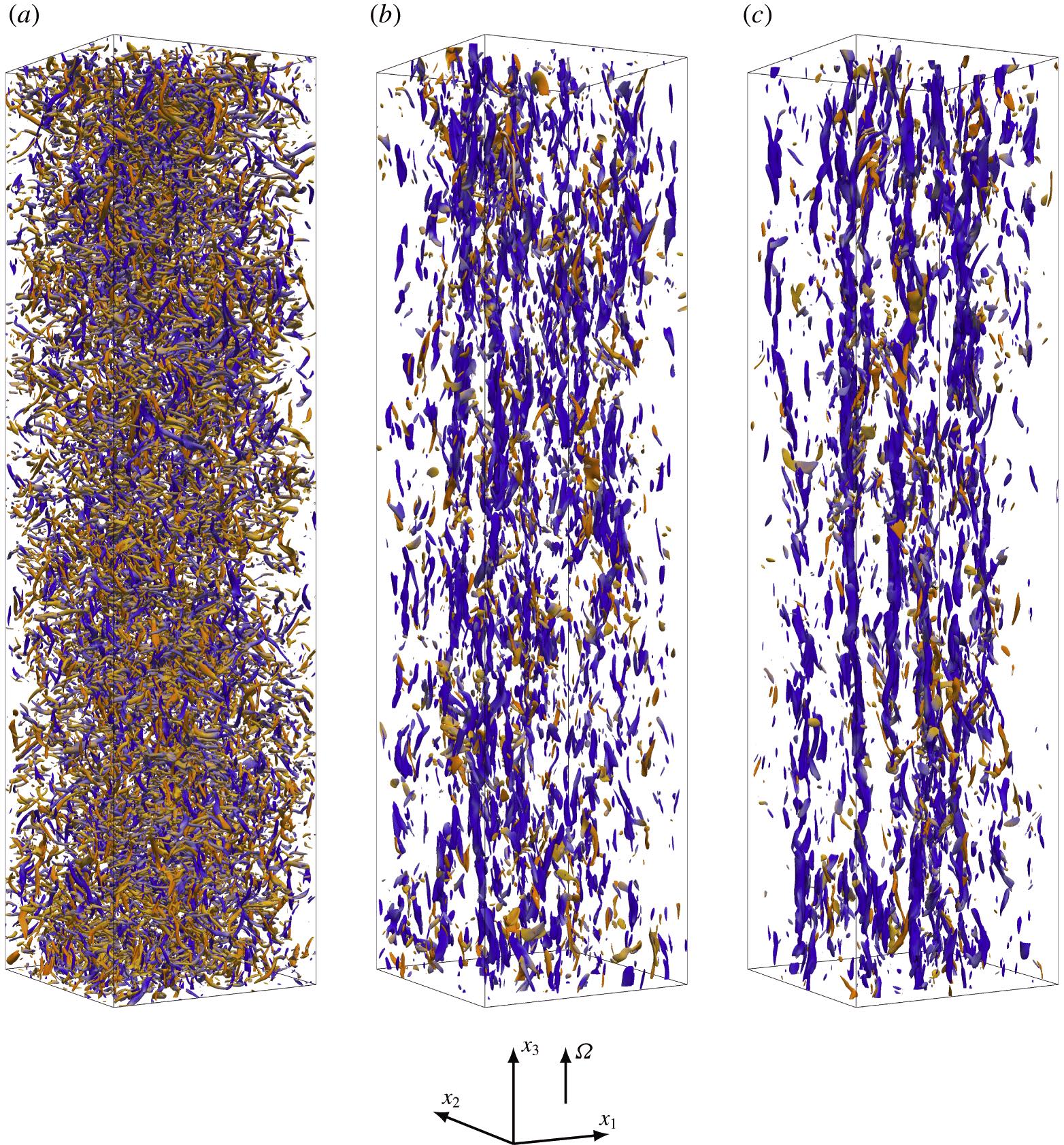
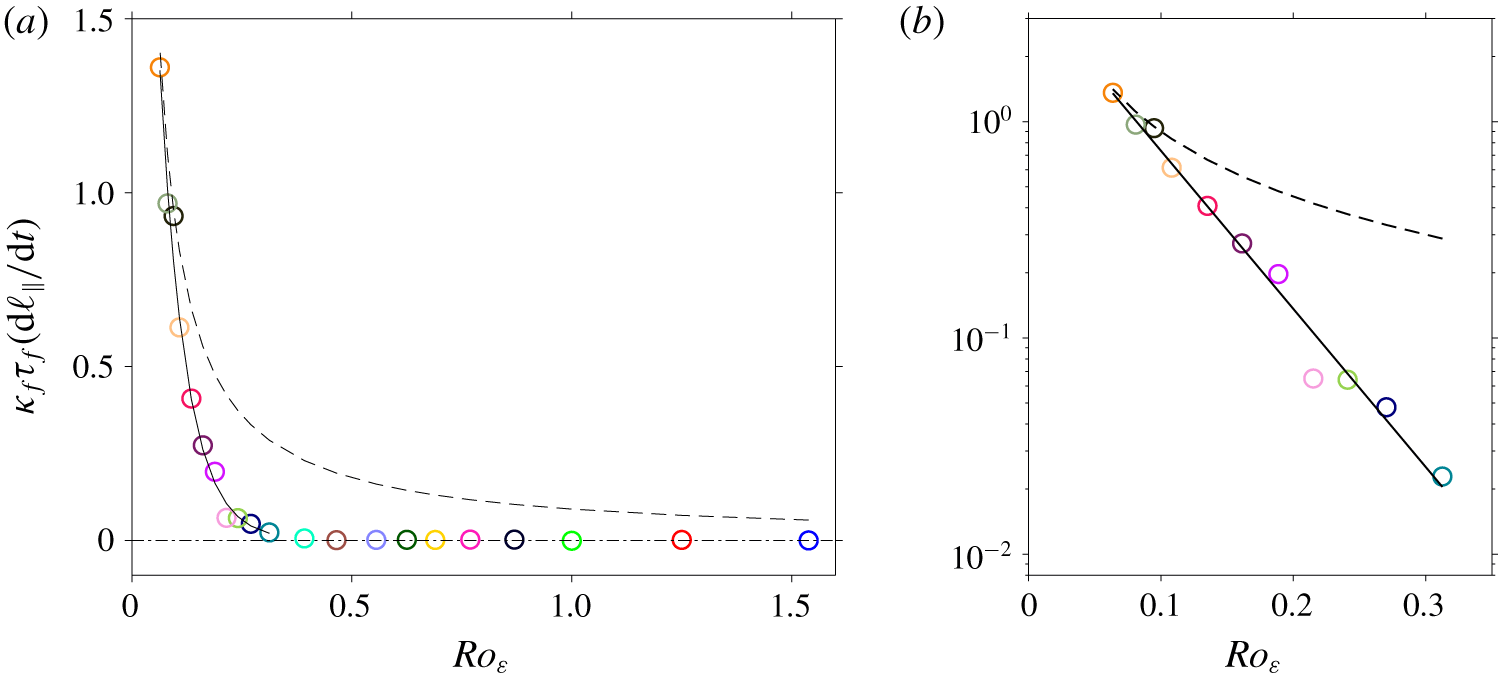
Two aspects of homogeneous rotating turbulence are quantified through forced direct numerical simulations in an elongated domain, which, in the direction of rotation, is approximately 340 times larger than the typical initial eddy size. First, by following the time evolution of the integral length scale along the axis of rotation $ℓ_{‖}$ , the growth rate of the columnar eddies and its dependence on the Rossby number $R o_{𝜀}$ is determined as $𝛾 = 3.90 \exp (- 16.72 R o_{𝜀})$ for $0.06 ⩽ R o_{𝜀} ⩽ 0.31$ , where $𝛾$ is the non-dimensional growth rate. Second, a scaling law for the energy dissipation rate $𝜀_{𝜈}$ is sought.

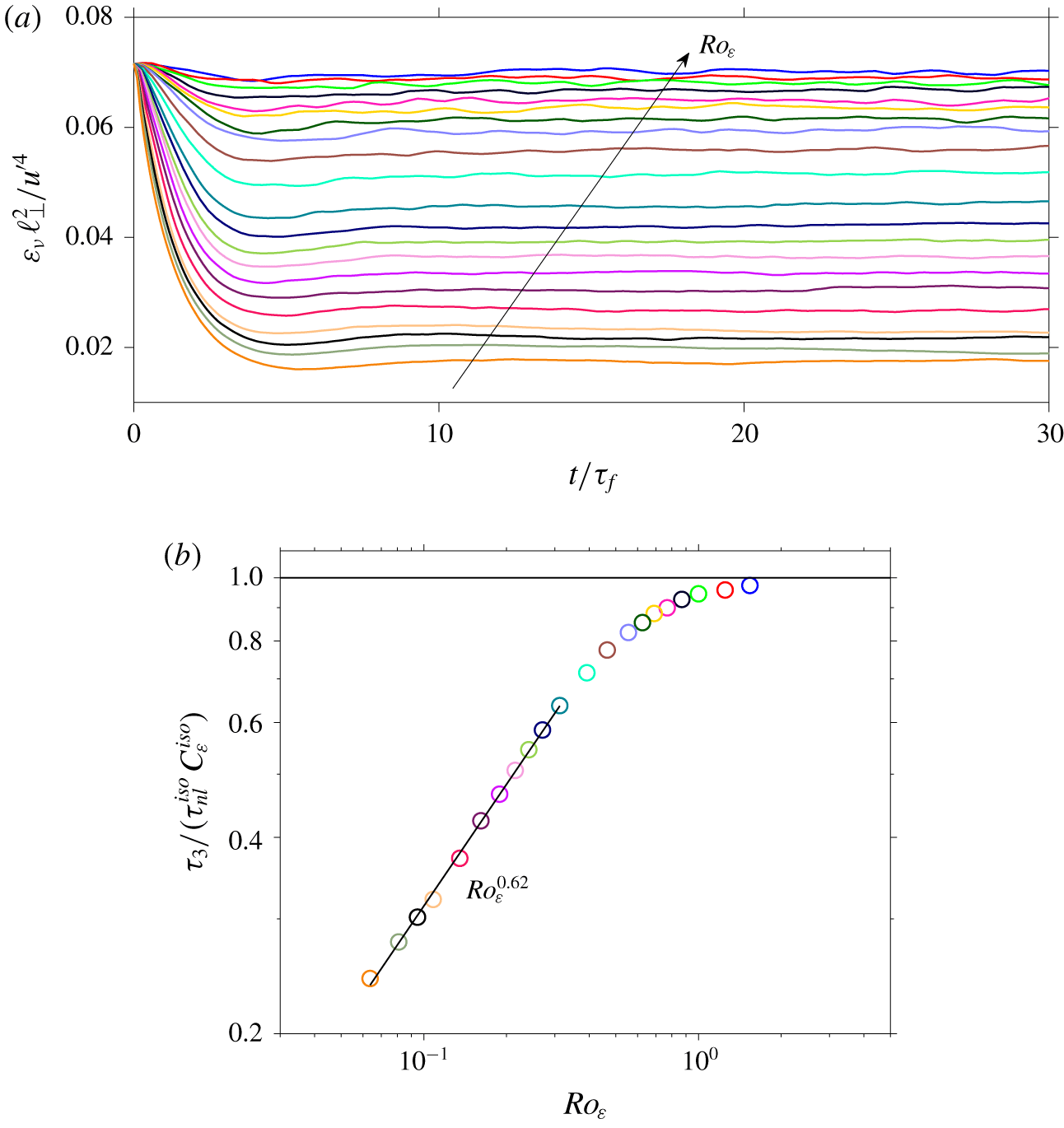
Comparison with current available scaling laws shows that the relation proposed by Baqui & Davidson (Phys. Fluids, vol. 27(2), 2015, 025107), i.e. $𝜀_{𝜈} \sim {u^{'}}^{3} / ℓ_{‖}$ , where $u^{'}$ is the root-mean-square velocity, approximates well part of our data, more specifically the range $0.39 ⩽ R o_{𝜀} ⩽ 1.54$ . However, relations proposed in the literature fail to model the data for the second and most interesting range, i.e. $0.06 ⩽ R o_{𝜀} ⩽ 0.31$ , which is marked by the formation of columnar eddies.

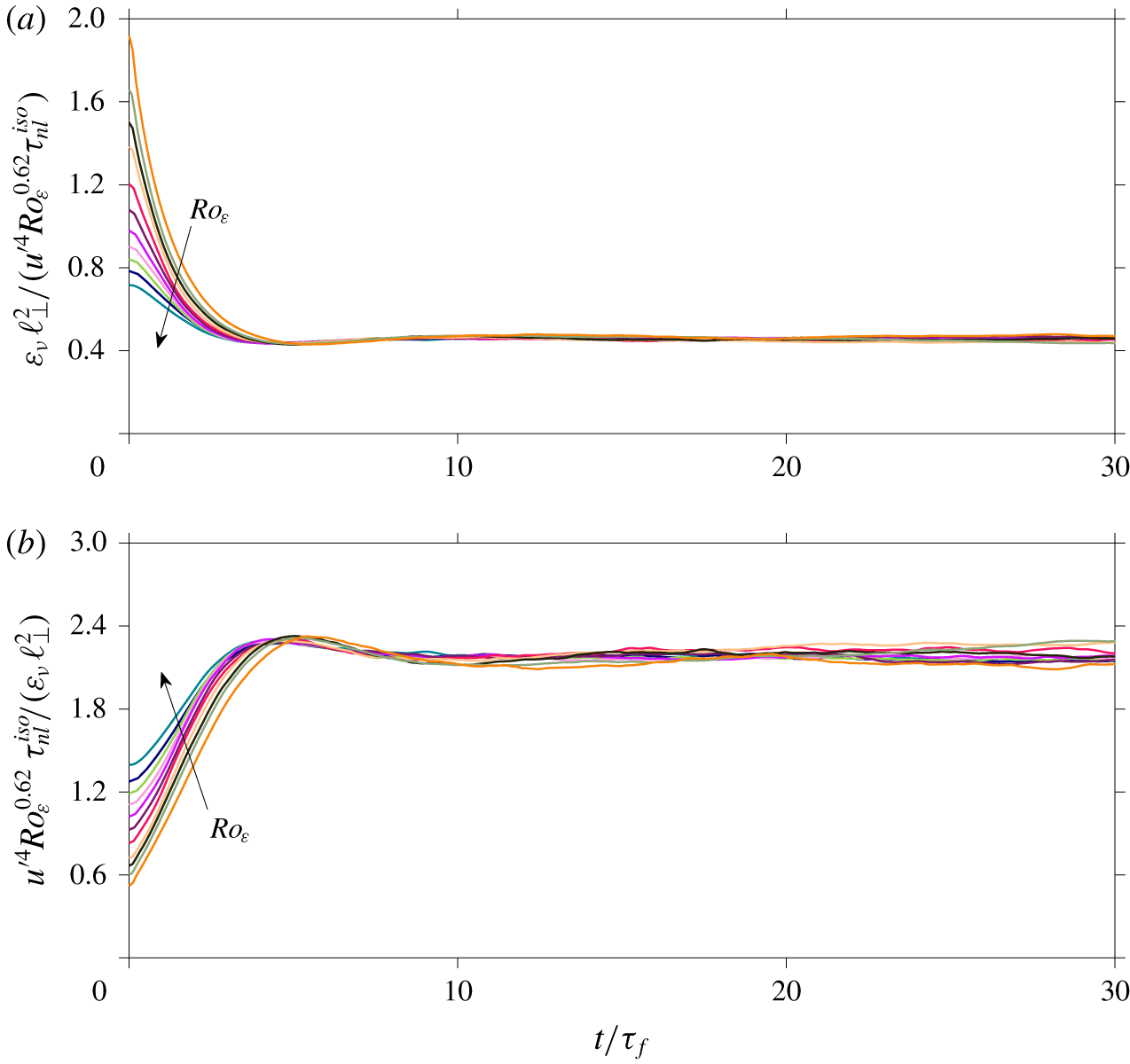
To find a similarity relation for the latter, we exploit the concept of a spectral transfer time introduced by Kraichnan (Phys. Fluids, vol. 8(7), 1965, p. 1385). Within this framework, the energy dissipation rate is considered to depend on both the nonlinear time scale and the relaxation time scale. Thus, by analysing our data, expressions for these different time scales are obtained that result in $𝜀_{𝜈} \sim (u^{' 4} R o_{𝜀}^{0.62} 𝜏_{n l}^{i s o}) / ℓ_{⊥}^{2}$ , where $ℓ_{⊥}$ is the integral length scale in the direction normal to the axis of rotation and $𝜏_{n l}^{i s o}$ is the nonlinear time scale of the initial homogeneous isotropic field.

Flow-field visualization of a subset of the computational domain (1/16 of the entire computational domain), showing half of the horizontal domain extension and a quarter of the vertical domain size. Iso-contours of the 𝑄-criterion colored by the normalized projection of the vorticity vector along the axis of rotation. Blue colours indicate structures that rotate in the same sense as 𝜴 (anticlockwise), whereas orange colours indicate the opposite sense of rotation (clockwise). (a) Isotropic initial condition. (b,c) The runs with 𝑅𝑜_𝜀=0.06 at two time instants after the onset of rotation.

Non-dimensional growth rate of the parallel integral length scale as function of the Rossby number 𝑅𝑜_𝜀. The least-squares fit (——) for the range 0.06⩽𝑅𝑜_𝜀⩽0.31 yields the power law 𝛾=𝑎 exp(𝑏𝑅𝑜_𝜀) with 𝑎=3.90 and 𝑏=−16.72. The thin dashed line (– – –) represents a law of the type 𝛾∼𝑅𝑜⁻¹𝜀, where the constant of proportionality was arbitrarily chosen to fit the leftmost data point. The dot-dashed line (– ⋅ – ⋅ –) represents a zero growth rate.

Decorrelation (relaxation) time scale 𝜏₃ (a) as a function of time and (b) averaged over the interval 10 ⩽ 𝑡/𝜏_𝑓⩽ 30 and normalized by the nonlinear time scale. Two reference lines are included in panel (b): the horizontal line shows that the relaxation time scale tends to the value of the nonlinear time scale of the homogeneous isotropic case for large 𝑅𝑜_𝜀; the other line shows a power-law dependence of the type 𝑅𝑜_𝜀^h with h = 0.62.

Verification for cases with strong rotation: time evolution of the energy dissipation rate normalized according to the proposed scaling laws.

Rossby-number effects on columnar eddy formation and the energy dissipation law in homogeneous rotating turbulence

Publications