A. Thari, V. Pasquariello, N. Aage, S. Hickel (2021)
Computers and Fluids 229: 105099. doi: 10.1016/j.compfluid.2021.105099
We present an adaptive reduced-order model for the efficient time-resolved simulation of fluid–structure interaction problems with complex and non-linear deformations. The model is based on repeated linearizations of the structural balance equations. Upon each linearization step, the number of unknowns is strongly decreased by using modal reduction, which leads to a substantial gain in computational efficiency.
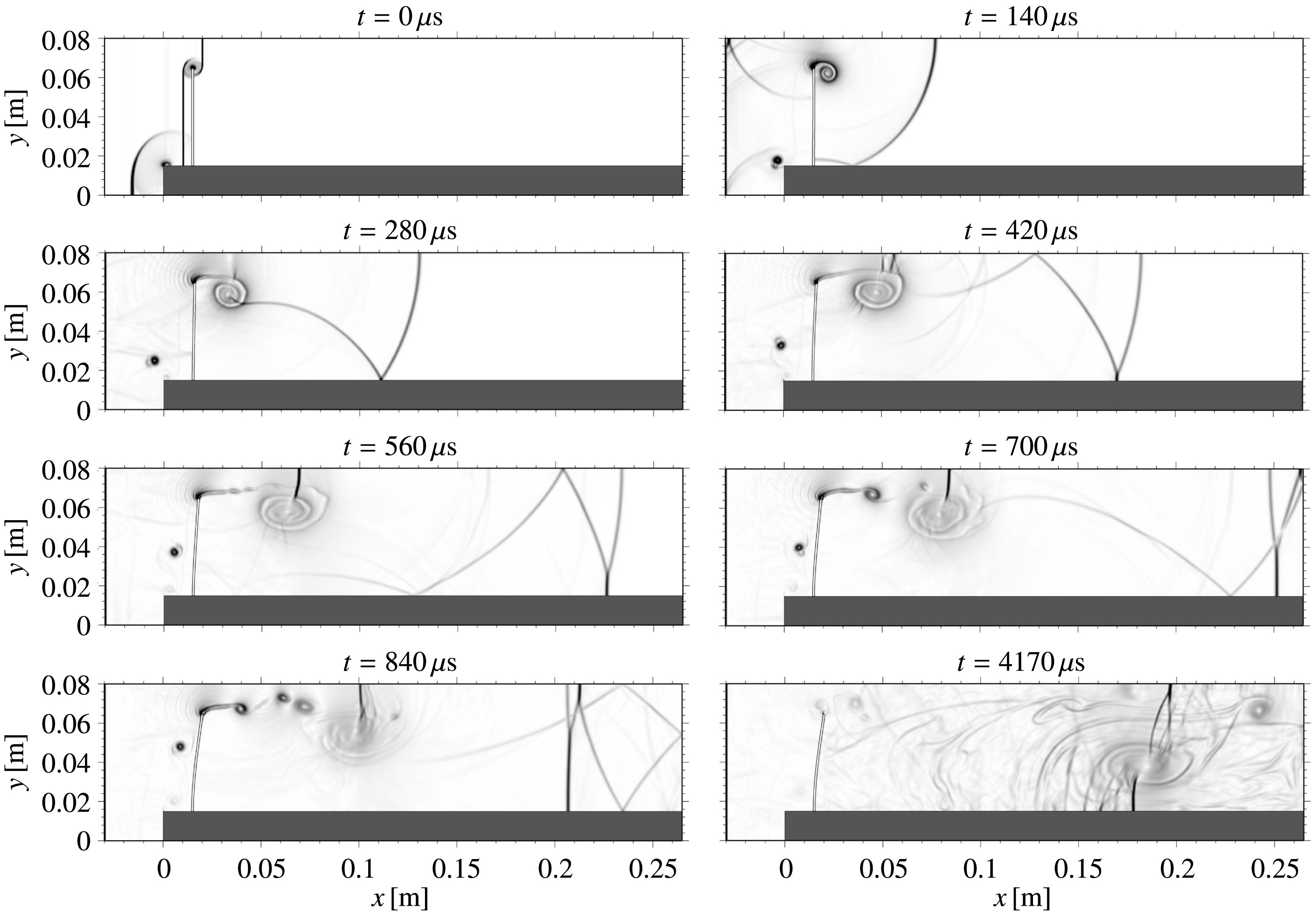
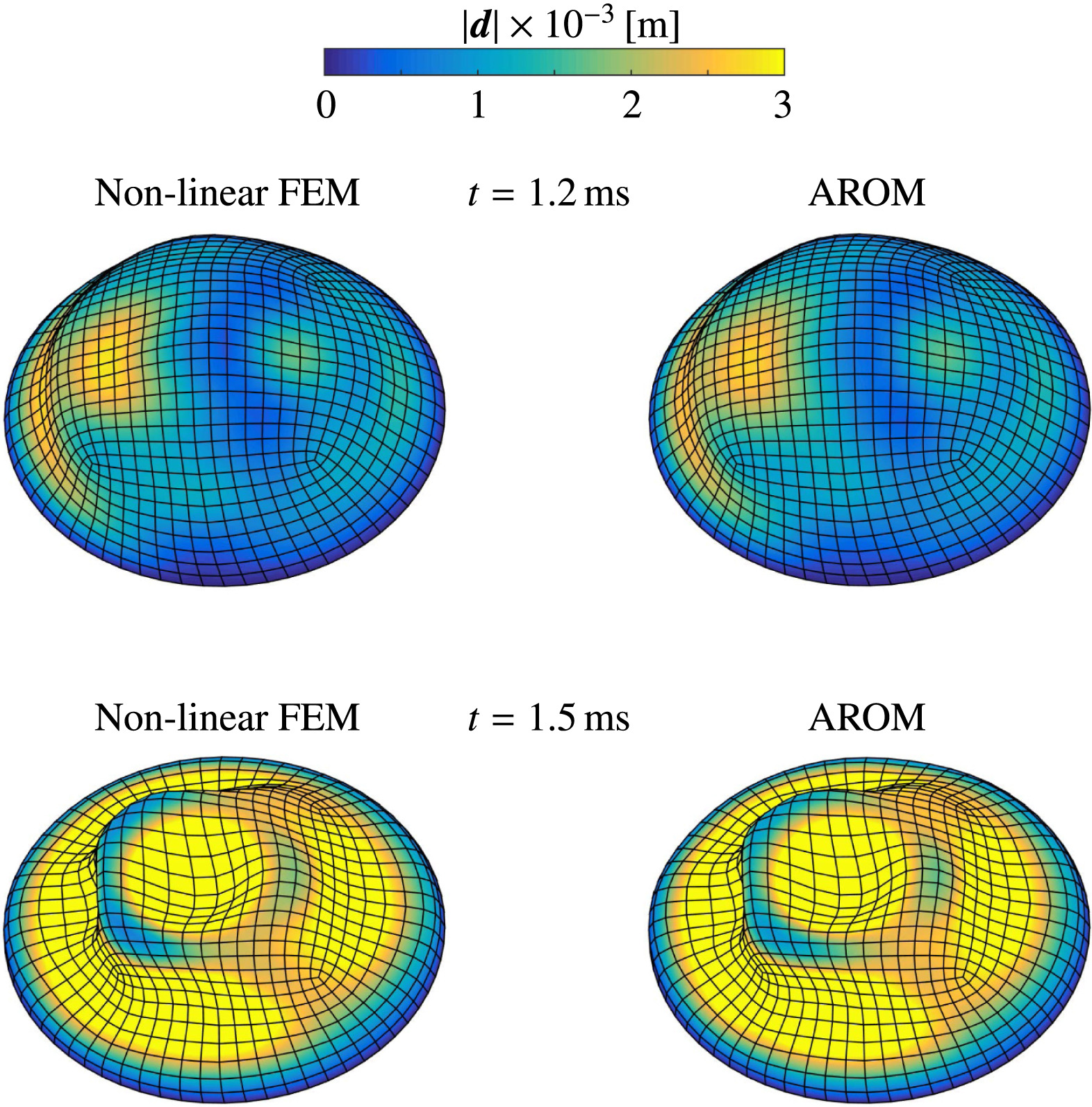
Through adaptive re-calibration and truncation augmentation whenever a non-dimensional deformation threshold is exceeded, we ensure that the reduced modal basis maintains arbitrary accuracy for small and large deformations. Our novel model is embedded into a partitioned, loosely coupled finite volume–finite element framework, in which the structural interface motion within the Eulerian fluid solver is accounted for by a conservative cut-element immersed-boundary method. Applications to the aeroelastic instability of a flat plate at supersonic speeds, to an elastic panel placed within a shock tube, and to the shock induced buckling of an inflated thin semi-sphere demonstrate the efficiency and accuracy of the method.