X. Li, S. Hulshoff, S. Hickel (2021)
Computer Methods in Applied Mechanics and Engineering 379: 113733. doi: 10.1016/j.cma.2021.113733
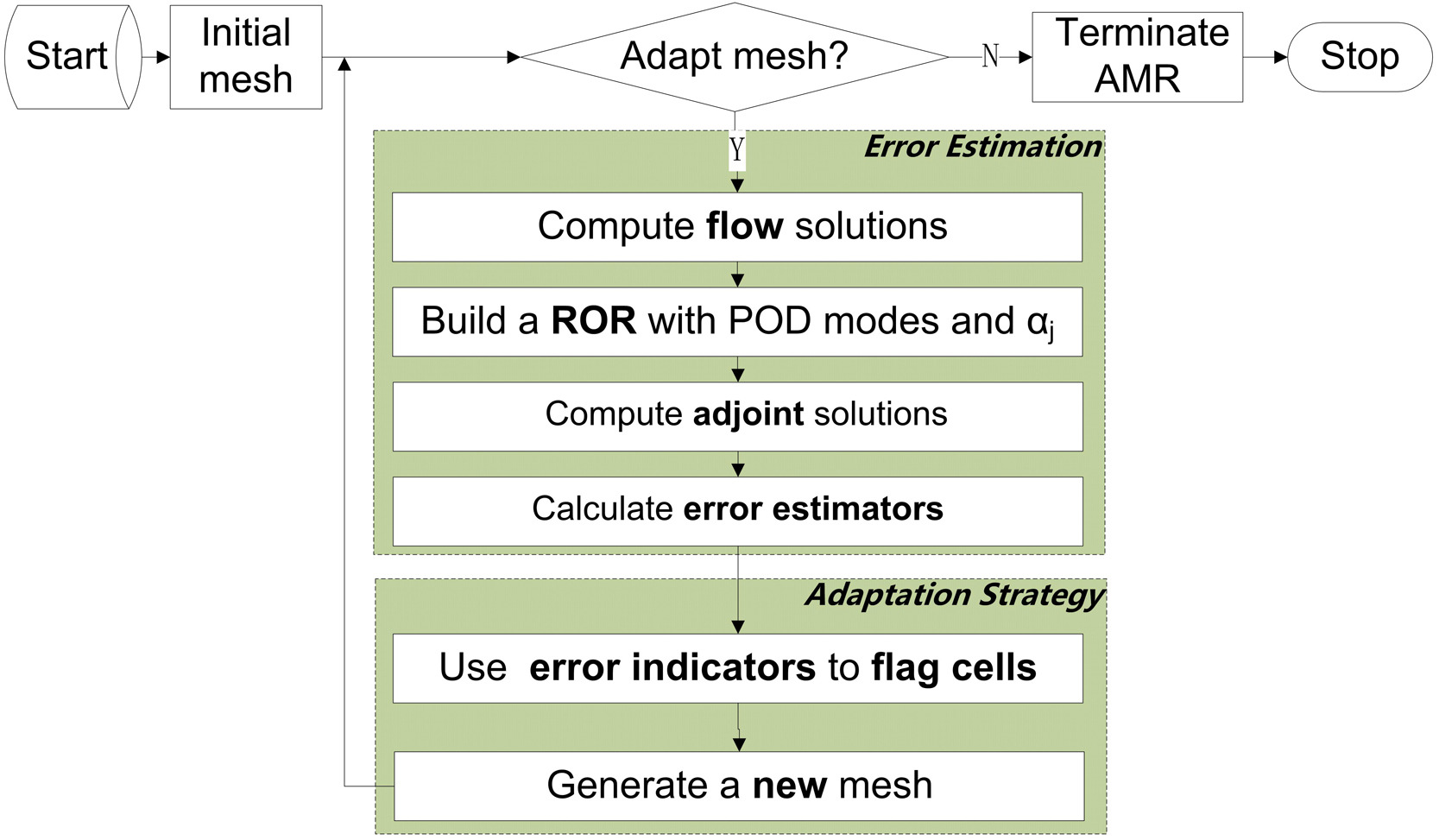
Adaptive Mesh Refinement (AMR) is potentially an effective way to automatically generate computational meshes for high-fidelity simulations such as Large Eddy Simulation (LES). When combined with adjoint methods, which are able to localize error contributions, AMR can generate meshes that are optimal for computing a physical quantity of interest (e.g. lift or drag).
In order to apply adjoint-based AMR techniques to LES, primal flow solutions are needed to solve the adjoint problem backward in time. However, the resources required to store primal flow solutions can be huge, even prohibitive, in practical problems because of the typically very fine meshes and long averaging times for computing the statistical quantities of interest. Here, a Reduced-Order Representation (ROR) based upon proper orthogonal decomposition is introduced to address this issue. We develop an Enhanced Online Algorithm (EOA) based on incremental singular value decomposition to build this ROR online, which makes adjoint-based AMR feasible for practical applications. An adjoint-based error estimation procedure is first introduced, and verified using a manufactured solution. Then a ROR-driven AMR strategy is studied using a 1D unsteady Burgers problem with a multi-frequency forcing term. This is also used to evaluate the EOA for ROR-driven AMR. Numerical results demonstrate that the enhanced online algorithm generates RORs that are sufficiently accurate for AMR, avoiding the storage of almost all of the primal solution data.