S. Hickel, N.A. Adams, J.A. Domaradzki (2006)
Journal of Computational Physics 213: 413-436. doi: 10.1016/j.jcp.2005.08.017
The adaptive local deconvolution method (ALDM) is proposed as a new nonlinear discretization scheme designed for implicit large-eddy simulation (ILES) of turbulent flows. In ILES the truncation error of the discretization of the convective terms functions as a subgrid-scale model. Therefore, the model is implicitly contained within the discretization, and an explicit computation of model terms becomes unnecessary.
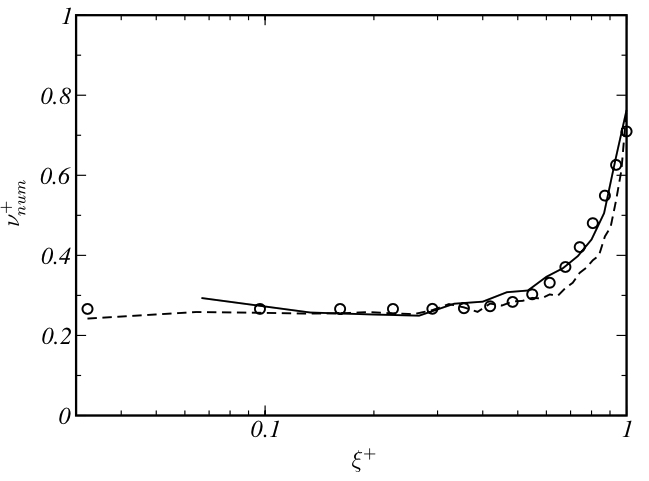
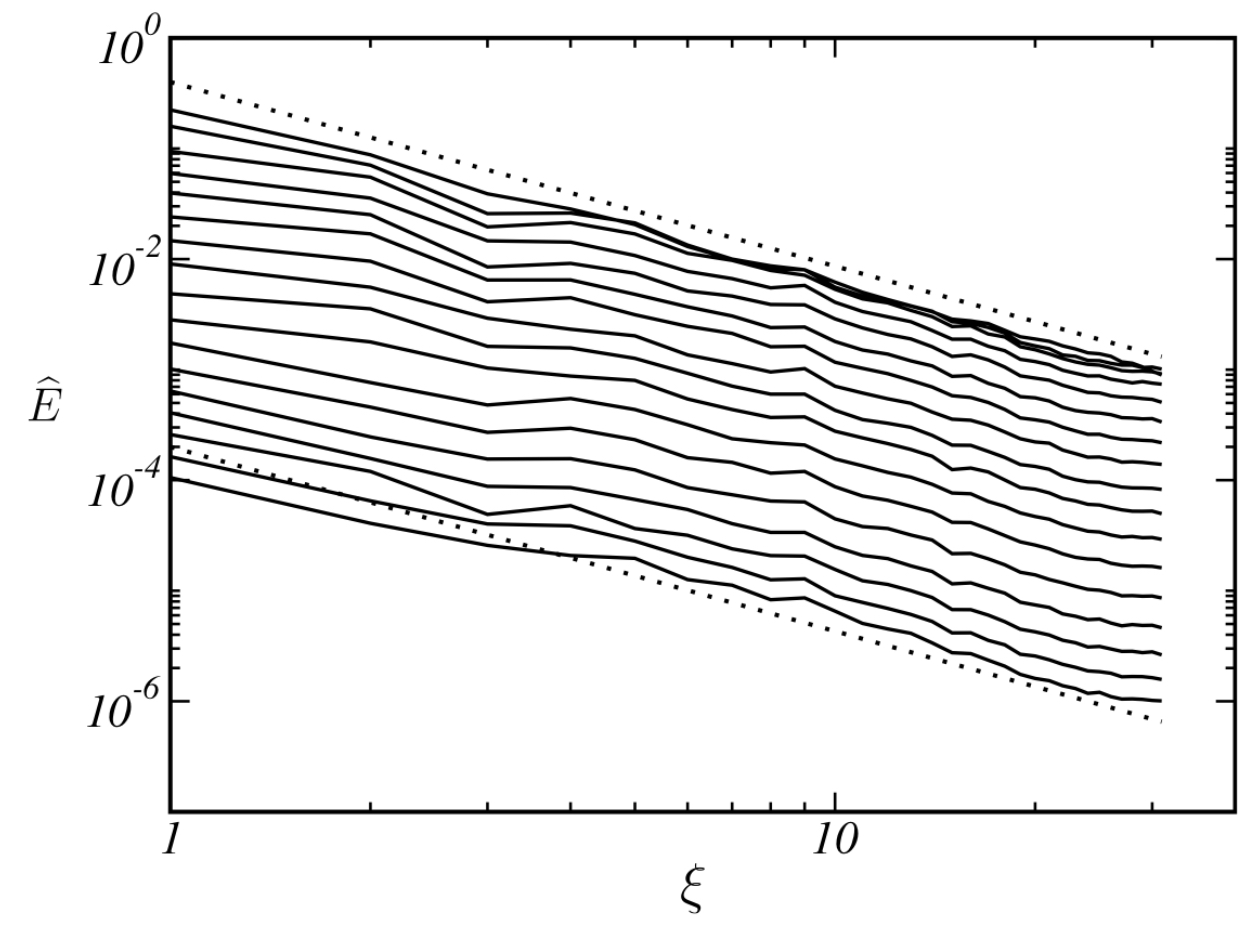
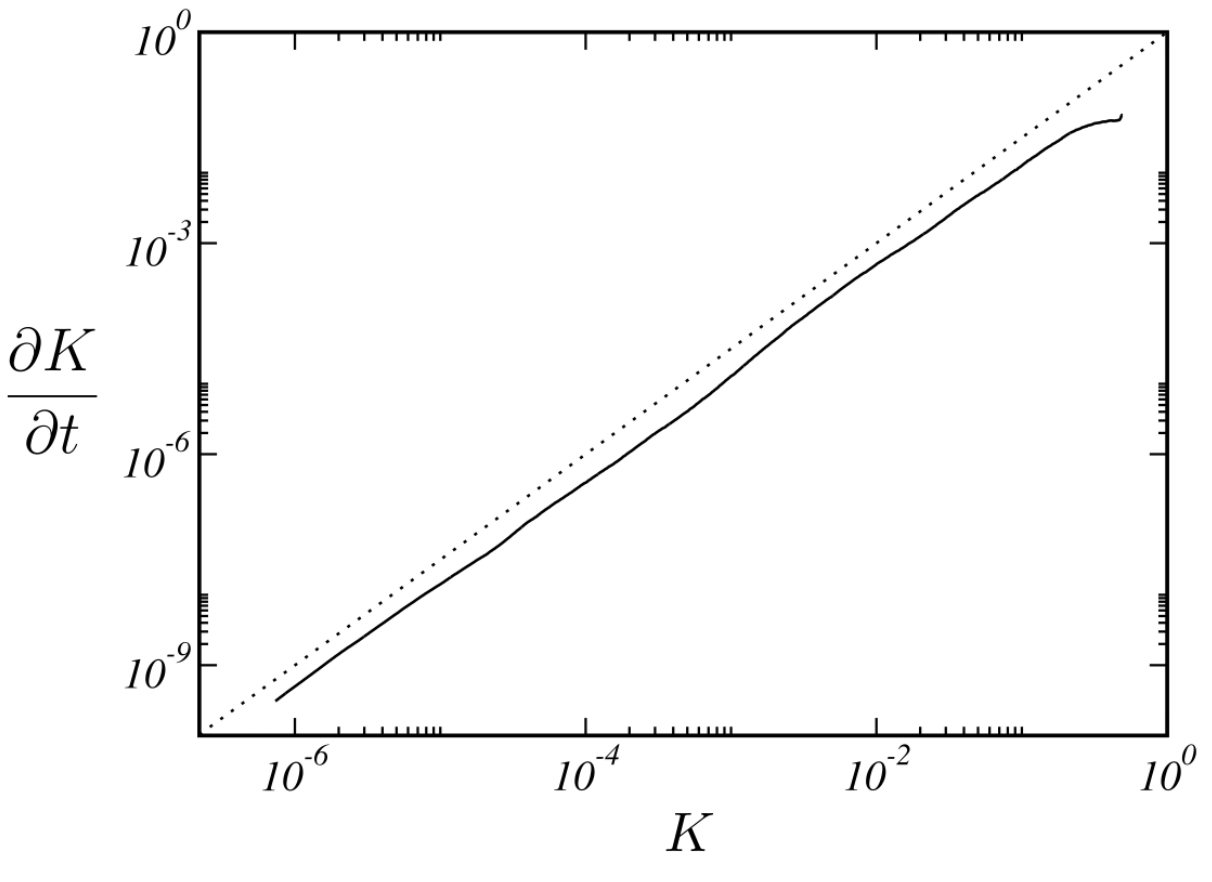
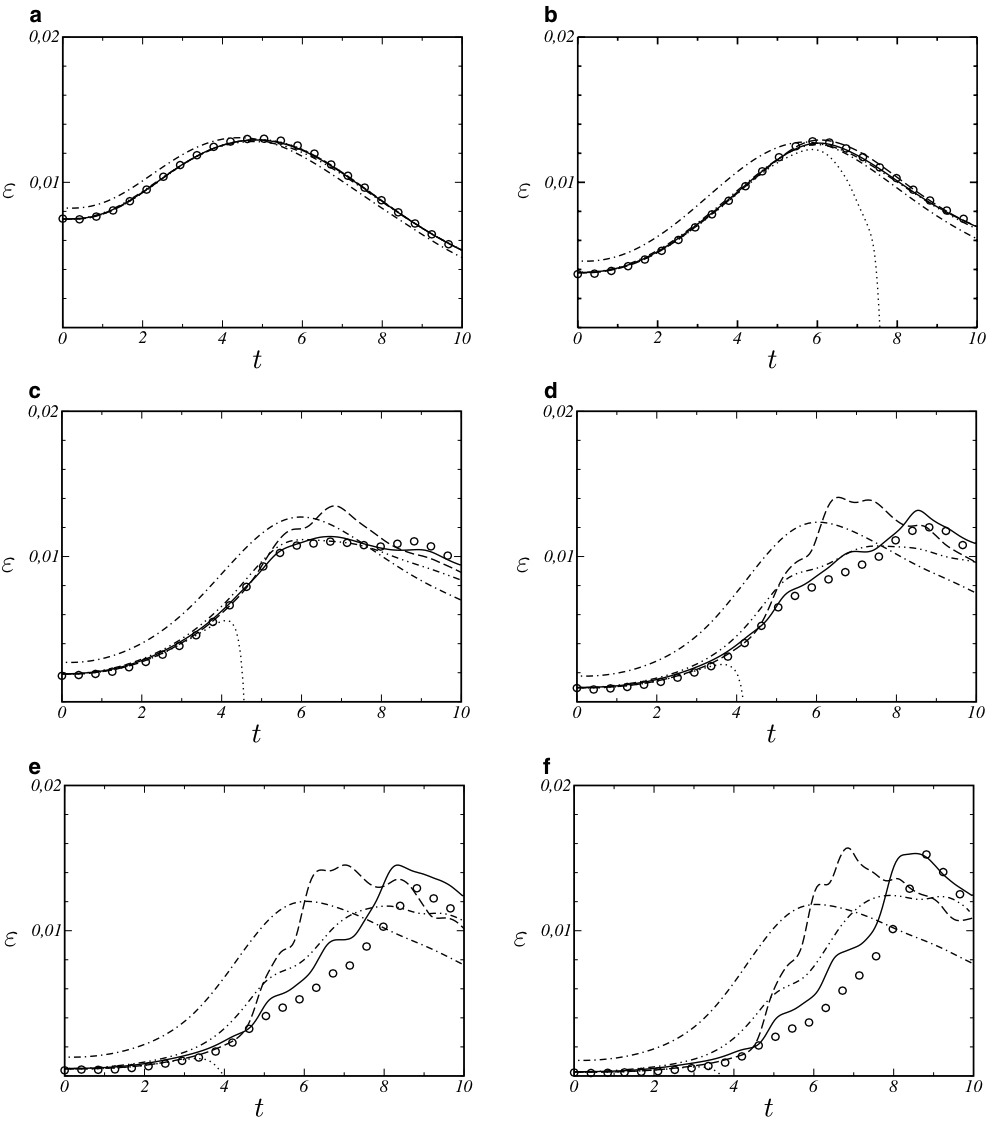
The discretization is based on a solution-adaptive deconvolution operator which allows to control the truncation error. Deconvolution parameters are determined by an analysis of the spectral numerical viscosity. An automatic optimization based on an evolutionary algorithm is employed to obtain a set of parameters which results in an optimum spectral match for the numerical viscosity with theoretical predictions for isotropic turbulence. Simulations of large-scale forced and decaying three-dimensional homogeneous isotropic turbulence show an excellent agreement with theory and experimental data and demonstrate the good performance of the implicit model. As an example for transitional flows, instability and breakdown of the three-dimensional Taylor–Green vortex are considered. The implicit model correctly predicts instability growth and transition to developed turbulence. It is shown that the implicit model performs at least as well as established explicit models.